Editor’s note: Matt Oguz is managing director of Palo Alto Venture Science.
When Nassim Nicholas Taleb developed his popular theory to explore way-out-of-the-norm surprising events, he outlined three characteristics of a black swan event:
- The event has a huge impact
- The event is very hard to explain using (commonly used) scientific methods
- The event appears unforeseen due to people’s psychological biases.
The black swan events are popular in venture capital, a unique asset class that historically has all three characteristics as Taleb outlined in his colorful book. What makes venture capital different from other asset classes is its complex qualitative and quantitative characteristics. The qualitative attributes are widely covered. The quantitative characteristics, not so much.
Numerical analysis had been more predominant in liquid assets such as stocks where historic returns are available. For example, if you put $50 in Google last year, you’d end up with $100 this year. You can see the same for AAPL or GE. From there, you can do a number of calculations such as overall returns in a portfolio made up of stocks or comparing their returns to a bundle of them, i.e. indexes.
Understanding returns and portfolio management concepts in liquid markets are quite clear thanks to Nobel Prize-winning economists such as Harry Markowitz. Unfortunately, Markowitz’s portfolio theory won’t work for venture capital because it turns out that VC returns are not normally distributed, a requirement for Markowitz to work.
For private companies, particularly in their early stages, numerical analysis is complex. The frame in which you look at startups is completely different from the one for liquid assets. Several years ago Fred Wilson started to explore in his blog what these returns look like. Taleb in his book calls the bell curve “that great intellectual fraud” and explains the situations that don’t demonstrate a bell curve. Unfortunately, he doesn’t dig deeper into what the non-bell curve looks like, and leads us to believe in a mystical situation that eventually leads to another cognitive bias: “nothing, particularly outliers, can be predicted, so let’s just focus on what we know.” On the contrary, non-Gaussian distributions are well-studied.
So a closer look at the distribution of returns in venture capital looks something like this:
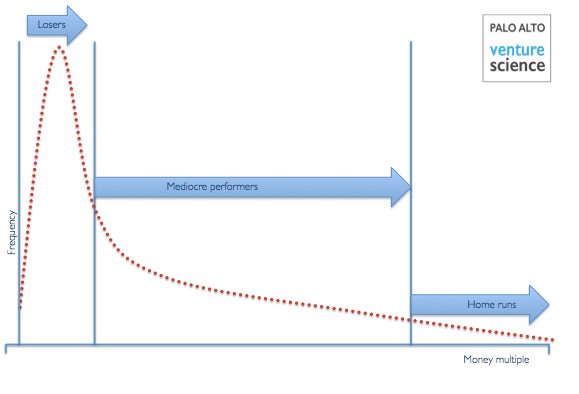
Traditional VC targets home runs to compensate for early losses.
This looks quite like what’s called a lognormal curve. The distribution actually resembles more of a log-levy distribution, a variant of lognormal but let’s stick with lognormal for simplicity. Here’s the academic description: A random variable X is said to have the lognormal distribution with parameters μ∈ℝ and σ∈(0,∞) if ln(X) has the normal distribution with mean μ and standard deviation σ. Equivalently, X=eY where Y is normally distributed with mean μ and standard deviation σ. The log of the random variable is normally distributed.
The lognormal distribution is used to model continuous random quantities when the distribution is believed to be skewed, such as certain income and lifetime variables. Only positive values are possible for the variable, and the distribution is skewed to the left (Gibrat, 1931). Limpert et al. has a great paper in this field named Lognormal Distributions across the Sciences: Keys and Clues. In that paper, Lambert et al. describe the characteristics of lognormal distribution beautifully and provide examples of lognormal events. Some of those are as follows:
- Latency periods of diseases
- Survival time after cancer diagnosis
- Crystals in ice cream
- Age of marriage
Income distribution (quite a popular subject these days):
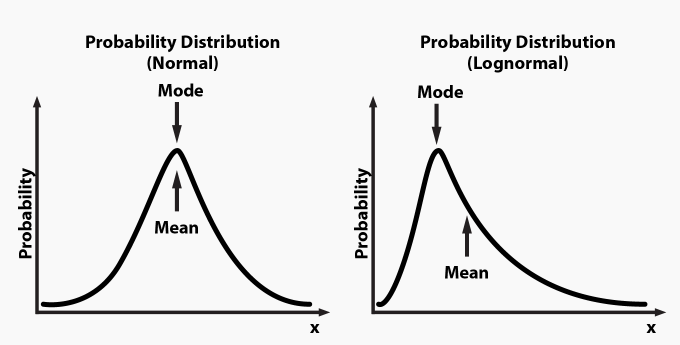
A random variable X is said to be lognormally distributed if log(X) is normally distributed. Lognormal curves describe the 80/20 situations better.
One may argue that the examples cited above don’t demonstrate extreme cases, i.e. black swans. But even in cases where “black swan” events exist, Benoit Mandelbrot, renowned professor of mathematical sciences at Yale, argued that log-levy distributions with longer tails are more appropriate.
The mathematical implications of the lognormal nature play into questions such as:
- How much we deploy to each startup we fund, i.e. guidance for check sizes
- Dry powder size i.e. cash reserves needed to make future investments
- Number of investments to make
- Distributing investments among funding stages
Elton and Gruber in their academic paper provide a good introduction to portfolio theory when investment relatives are lognormally distributed. If we assume that the returns are normal, and turns out they are not, then all of our calculations will be way off, including check size, re-ups, and dry powder. Analyzing returns based on their lognormal distribution characteristics provides great guidance to us and leads us to more rational decisions in how we deploy capital. As we start investing and realizing returns or losses, we’ll have a much better understanding of where the overall fund returns will end up. From there, we can adjust the size of our investments or bets.
The late John Lintner, a Nobel Prize winner and professor of economics at Harvard, showed in his earlier work that security and portfolio returns are better modeled by a lognormal distribution than a normal distribution. Levy, Bawa and Chakrin later showed that for lognormal distributions investors would choose their portfolios from a mean logarithmic variance efficient frontier. The lognormal nature of the returns provide good guidance for the downside of a portfolio as we construct the probability distribution for the entire portfolio by computing a series of convolution integrals.
The check-size problem for instance is common in venture capital. Let’s say a company is raising a $10 million round. How much do you participate? $2 million, $3 million, more? The real problem here is how to maximize gains based on the the assumption that we’ll make more of these investments, the size of our pool of capital and the probability distribution of returns and failures.
John Kelly, who worked at Bell Labs, developed Kelly Criterion in 1956 to tackle long distance telephone signal noise issues. Kelly later teamed up with Claude Shannon, who is famous for having founded information theory, digital computer and digital circuit design theories. Ed Thorpe, an MIT math-professor-turned-blackjack-player turned multibillion dollar hedge fund manager utilized Kelly Criterion to optimize his investment sizes in both blackjack and then in a “safer” gaming environment, the Wall Street. Thorpe’s blackjack adventure became the basis for the MIT blackjack team and made it to the big screen in the movie 21.
Unfortunately, Thorpe’s much more successful hedge fund did not receive popular coverage. PIMCO’s Bill Gross is also a huge proponent of Kelly Criterion and his accomplishments are stellar. Since we understand the nature of the returns, expanding Kelly to venture capital is quite possible. Solving a Kelly variant assuming a lognormal distribution helps drive rational answers to questions such as check size or dry powder calculations.
One major implication of the return multiples resembling a lognormal curve is that the more errors we make early in the game, the less likely we are to hit a homerun. On the qualitative end of this analysis, to get to better returns we must somehow cut the “excess fat” from the top of this curve and add it to the tail. It seems like if we can do that: a. our returns will improve and b. we’ll end up better prepared for a home-run.
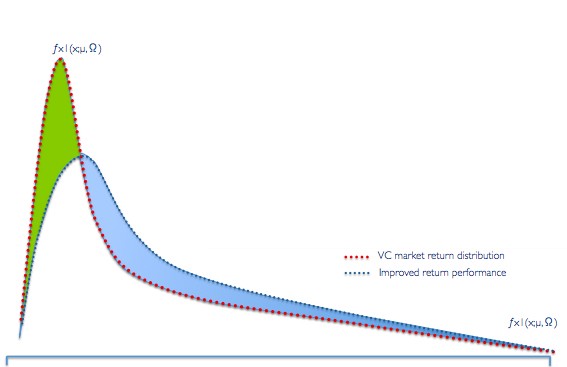
Using decision models to have a disciplined selection process helps minimize cognitive errors. The VC industry is prone to “black swan” events due to its high propensity for cognitive biases, one of the three characteristics of a black swan.
Avoiding decision errors would certainly improve our returns, or “add alpha” as jargoned in finance. In an earlier article, I outlined a number of errors generally committed in venture capital such as anchoring, availability bias, recency, unit bias — accepting valuations as “universal,” group thinking (bandwagon effect) — following the herd, cognitive inertia — unwillingness to change thought patterns, irrational escalation — re-upping investment even though one knows it’s a bad one, and overconfidence.
The presence of decision biases is one of the three characteristics of a black swan event. The other two are large impact of the event and not being able to model the probability of the event. So if we’re after a black swan, on the upside, avoiding cognitive errors earlier on should lead to thicker tails thereby increasing the chances of a home run.
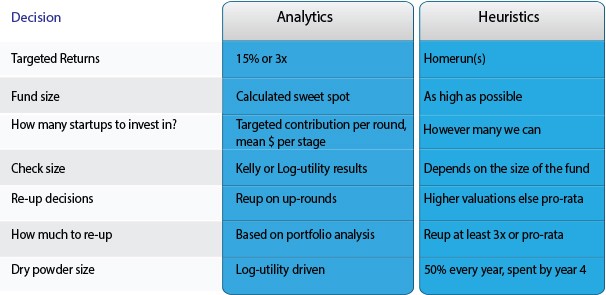
Key venture capital decisions using analytics vs. (popular) heuristics.
The events on the end of the lognormal tail are where big return multiples are and their returns are substantially higher than average returns. Even though cognitive biases are common in venture capital decision-making, particularly in capital deployment, the benefits of a disciplined approach are clear. As we see looking at past returns, “soft” characteristics of fund management such as deal-flow, value-add, etc. have not delivered the 3x+ returns on a consistent basis regardless of the VC firm.
A comprehensive study of the economic nature of venture capital is a must in every VC firm from here on out. In our case, understanding the statistical distribution of returns provides guidelines around how we deploy capital instead of arbitrary rules-of-thumb.
As John Arbuthnot said, “Mathematical knowledge adds vigour to the mind, frees it from prejudice, credulity, and superstition” and as we build companies based on math and engineering every day, that is exactly where venture capital needs to be.
