One of the reasons artificial intelligence is such an interesting field is that pretty much no one knows what it might turn out to be good at. Two papers by leading labs published in the journal Nature today show that machine learning can be applied to tasks as technically demanding as protein generation and as abstract as pure mathematics.
The protein thing may not sound like much of a surprise given the recent commotion around AI’s facility in protein folding, as demonstrated by Google’s DeepMind and the University of Washington’s Baker Lab, not coincidentally also the ones who put out the papers we’re noting today.
The study from the Baker Lab shows that the model they created to understand how protein sequences are folded can be repurposed to essentially do the opposite: create a new sequence meeting certain parameters and which acts as expected when tested in vitro.
This wasn’t necessarily obvious — you might have an AI that’s great at detecting boats in pictures but can’t draw one, for instance, or an AI that translates Polish to English but not vice versa. So the discovery that an AI built to interpret the structure of proteins can also make new ones is an important one.
There has already been some work done in this direction by various labs, such as ProGen over at SalesForce Research. But Baker Lab’s RoseTTAFold and DeepMind’s AlphaFold are way out in front when it comes to accuracy in proteomic predictions, so it’s good to know the systems can turn their expertise to creative endeavors.
AI abstractions
Meanwhile, DeepMind captured the cover of Nature with a paper showing that AI can aid mathematicians in complex and abstract tasks. The results won’t turn the math world on its head, but they are truly novel and truly due to the help of a machine learning model, something that has never happened before.
The idea here relies on the fact that mathematics is largely the study of relationships and patterns — as one thing increases, another decreases, say, or as the faces of a polyhedron increase, so too does the number of its vertices. Because these things happen according to systems, mathematicians can arrive at conjectures about the exact relationship between those things.
Some of these ideas are simple, like the trigonometry expressions we learned in grade school: It’s a fundamental quality of triangles that the sum of their internal angles adds up to 180 degrees, or that the sum of the squares of the shorter sides is equal to the square of the hypotenuse. But what about for a 900-sided polyhedron in 8-dimensional space? Could you find the equivalent of a2 + b2 = c2 for that?
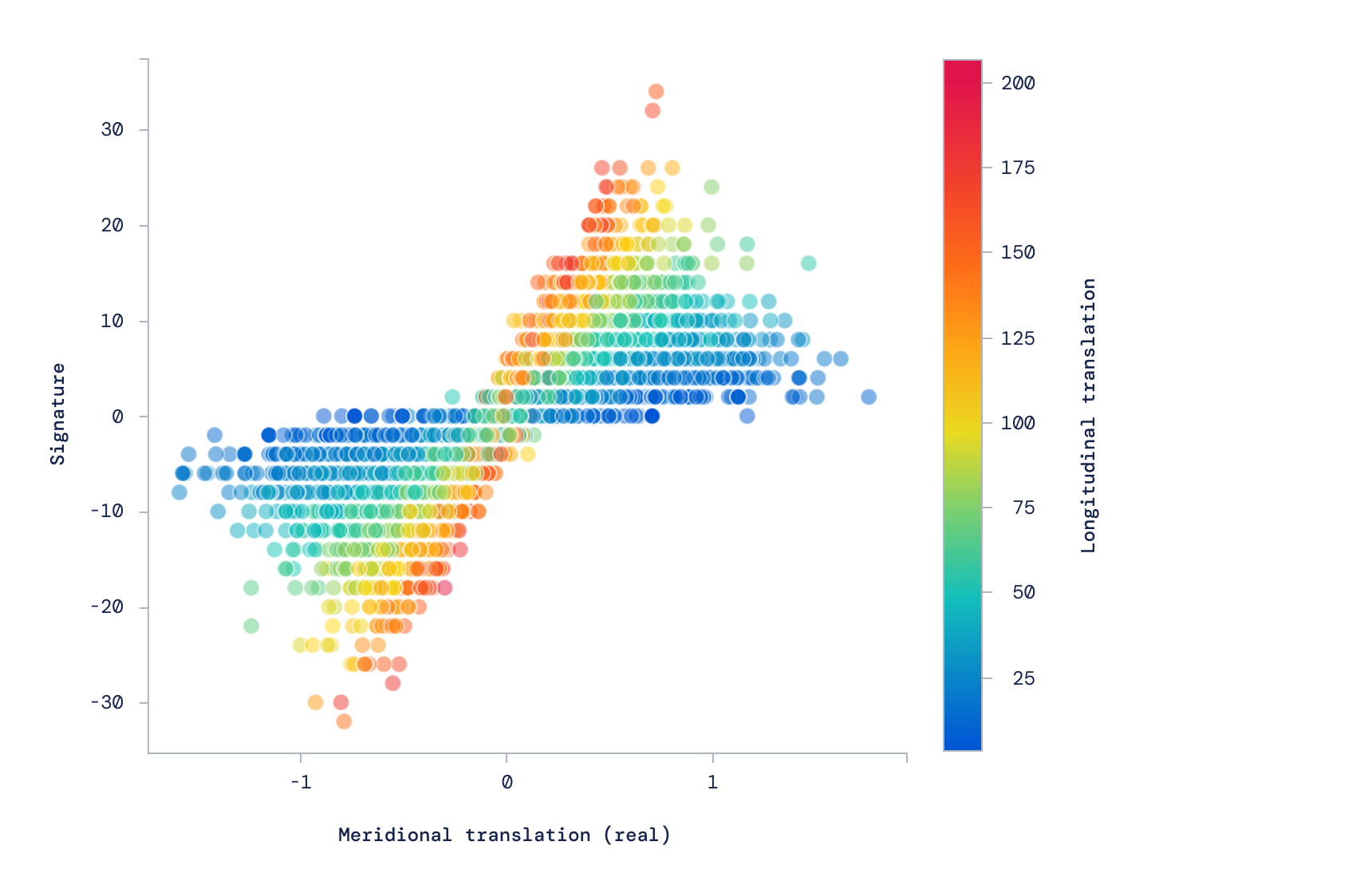
An example of the relationship between two complex qualities of knots: their geometry and algebraic signature. Image Credits: DeepMind
Mathematicians do, but there are limits to the amount of such work they can do, simply because one must evaluate many examples before one can be sure that a quality observed is universal and not coincidental. It is here, as a labor-saving method, that DeepMind deployed its AI model.
“Computers have always been good at spewing out data at a scale that humans can’t match but what is different [here] is the ability of AI to pick out patterns in the data that would have been impossible to detect on a human scale,” explained Oxford professor of mathematics Marcus du Sautoy in the DeepMind news release.
Now, the actual accomplishments made with the help of this AI system are miles above my head, but the mathematicians among our readers will surely understand the following, quoted from DeepMind:
Defying progress for nearly 40 years, the combinatorial invariance conjecture states that a relationship should exist between certain directed graphs and polynomials. Using ML techniques, we were able to gain confidence that such a relationship does indeed exist and to hypothesize that it might be related to structures known as broken dihedral intervals and extremal reflections. With this knowledge, Professor Williamson was able to conjecture a surprising and beautiful algorithm that would solve the combinatorial invariance conjecture.
Algebra, geometry, and quantum theory all share unique perspectives on [knots] and a long standing mystery is how these different branches relate: for example, what does the geometry of the knot tell us about the algebra? We trained an ML model to discover such a pattern and surprisingly, this revealed that a particular algebraic quantity — the signature — was directly related to the geometry of the knot, which was not previously known or suggested by existing theory. By using attribution techniques from machine learning, we guided Professor Lackenby to discover a new quantity, which we call the natural slope, that hints at an important aspect of structure overlooked until now.
The conjectures were borne out with millions of examples — another advantage of computation, that you can tell it to rigorously test your hypothesis without buying it pizza and coffee.
The DeepMind researchers and the professors mentioned above worked closely together to come up with these specific applications, so we’re not looking at a “universal pure math helper” or anything like that. But as Ruhr University Bochum’s Christian Stump notes in the Nature summary of the article, that it works at all is an important step toward such an idea.
“Neither result is necessarily out of reach for researchers in these areas, but both provide genuine insights that had not previously been found by specialists. The advance is therefore more than the outline of an abstract framework,” he wrote. “Whether or not such an approach is widely applicable is yet to be determined, but Davies et al. provide a promising demonstration of how machine-learning tools can be used to support the creative process of mathematical research.”
